A polarizáció az antennák egyik alapvető jellemzője. Először is meg kell értenünk a síkhullámok polarizációját. Ezután megvitathatjuk az antennapolarizáció főbb típusait.
lineáris polarizáció
Elkezdjük megérteni a sík elektromágneses hullám polarizációját.
Egy síkbeli elektromágneses (EM) hullámnak számos jellemzője van. Az első az, hogy a teljesítmény egy irányban terjed (két ortogonális irányban nem változik a tér). Másodszor, az elektromos és a mágneses tér merőleges egymásra és ortogonális egymásra. Az elektromos és a mágneses mezők merőlegesek a síkhullám terjedési irányára. Példaként vegyünk egy egyfrekvenciás elektromos mezőt (E mezőt), amelyet az (1) egyenlet ad meg. Az elektromágneses mező a +z irányban terjed. Az elektromos mező a +x irányba mutat. A mágneses mező a +y irányba mutat.
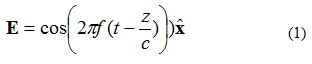
Az (1) egyenletben figyeljük meg a jelölést: . Ez egy egységvektor (egy hosszvektor), amely azt jelenti, hogy az elektromos térerősség pontja az x irányban van. A síkhullámot az 1. ábra szemlélteti.
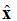
1. ábra. A +z irányban terjedő elektromos tér grafikus ábrázolása.
A polarizáció az elektromos tér nyomvonalának és terjedési alakjának (kontúrjának) leírása. Példaként vegyük az (1) síkhullámú elektromos tér egyenletét. Megvizsgáljuk az (X,Y,Z) = (0,0,0) elektromos tér pozícióját az idő függvényében. A tér amplitúdóját a 2. ábra ábrázolja, több időpontban. A tér "F" frekvencián oszcillál.
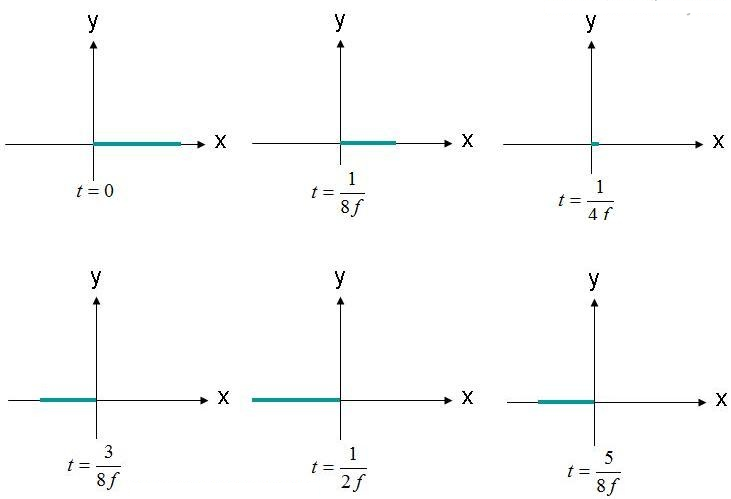
2. ábra. Figyeljük meg az (X, Y, Z) = (0,0,0) elektromos mezőt különböző időpontokban.
Az elektromos mezőt az origóban figyeljük meg, amplitúdójában előre-hátra oszcillálva. Az elektromos mező mindig a jelzett x tengely mentén helyezkedik el. Mivel az elektromos mező egyetlen vonal mentén helyezkedik el, ezt a mezőt lineárisan polarizáltnak mondhatjuk. Továbbá, ha az X tengely párhuzamos a talajjal, akkor ezt a mezőt vízszintesen polarizáltnak is nevezzük. Ha a mező az Y tengely mentén helyezkedik el, akkor a hullámot függőlegesen polarizáltnak mondhatjuk.
A lineárisan polarizált hullámoknak nem kell vízszintes vagy függőleges tengely mentén haladniuk. Például egy olyan elektromos térhullám, amelynek a korlátja egy vonal mentén fekszik, ahogy a 3. ábrán látható, szintén lineárisan polarizált lenne.
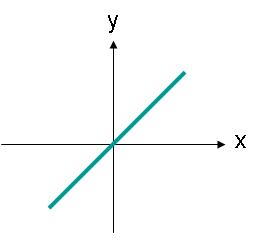
3. kép. Egy lineárisan polarizált hullám elektromos térerősség-amplitúdója, amelynek pályája egy szög.
A 3. ábrán látható elektromos mező a (2) egyenlettel írható le. Ekkor az elektromos mezőnek van egy x és egy y komponense. Mindkét komponens azonos méretű.
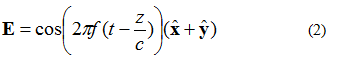
A (2) egyenlettel kapcsolatban érdemes megjegyezni az xy-komponenst és az elektronikus tereket a második szakaszban. Ez azt jelenti, hogy mindkét komponensnek mindenkor azonos az amplitúdója.
körkörös polarizáció
Most tegyük fel, hogy a síkhullám elektromos mezejét a (3) egyenlet adja meg:
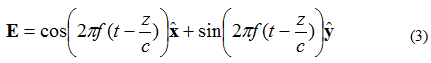
Ebben az esetben az X és Y elemek 90 fokkal eltérnek egymástól a fázistól. Ha a mezőt ismét (X, Y, Z) = (0,0,0) alakban figyeljük meg, mint korábban, az elektromos mező időfüggvénye a 4. ábrán látható módon fog kinézni.
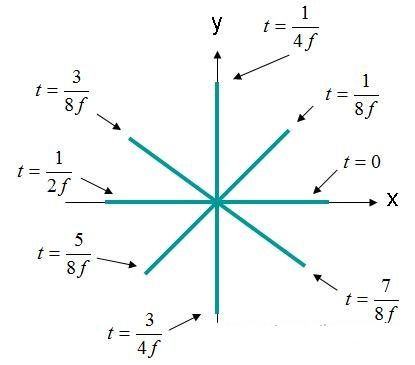
4. ábra. Elektromos térerősség (X, Y, Z) = (0,0,0) EQ tartomány. (3).
A 4. ábrán látható elektromos mező körben forog. Ezt a típusú mezőt cirkulárisan polarizált hullámként írják le. A cirkuláris polarizációhoz a következő kritériumoknak kell teljesülniük:
- Kör alakú polarizáció szabványa
- Az elektromos térnek két ortogonális (egymásra merőleges) komponensből kell állnia.
- Az elektromos tér ortogonális komponenseinek azonos amplitúdóval kell rendelkezniük.
- A kvadratúra komponenseknek 90 fokkal el kell mozdulniuk a fázistól.
Ha a 4. hullámú képernyőn haladunk, a mező forgását az óramutató járásával ellentétesnek és jobbra cirkulárisan polarizáltnak (RHCP) mondjuk. Ha a mezőt az óramutató járásával megegyező irányba forgatjuk, akkor a mező balra cirkulárisan polarizált (LHCP) lesz.
Elliptikus polarizáció
Ha az elektromos térnek két merőleges, egymásra 90 fokkal eltérő fázisú, de azonos nagyságú komponense van, akkor a tér elliptikusan polarizált lesz. Tekintsük a +z irányban terjedő síkhullám elektromos terét, amelyet a (4) egyenlet ír le:
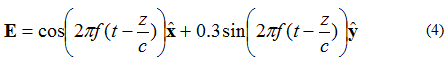
Az elektromos térerő vektorának csúcsa helyét az 5. ábra mutatja.
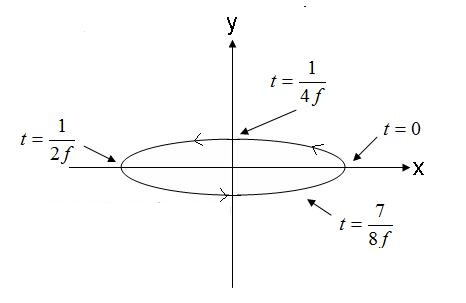
5. ábra. Prompt elliptikus polarizációs hullám elektromos mező. (4).
Az 5. ábrán látható, az óramutató járásával ellentétes irányban terjedő tér jobbra elliptikus lenne, ha a képernyőből kifelé haladna. Ha az elektromos tér vektora az ellenkező irányba forog, a tér balra elliptikusan polarizált lesz.
Továbbá az elliptikus polarizáció az excentricitására utal. Az excentricitás és a fő- és melléktengelyek amplitúdójának aránya. Például a (4) egyenletből származó hullám excentricitása 1/0,3 = 3,33. Az elliptikusan polarizált hullámokat a főtengely iránya írja le tovább. A (4) hullámegyenlet tengelye elsősorban az x tengelyből áll. Megjegyezzük, hogy a főtengely bármilyen síkszöget zárhat be. A szög nem szükséges az X, Y vagy Z tengelyhez illeszkedéshez. Végül fontos megjegyezni, hogy mind a kör-, mind a lineáris polarizáció az elliptikus polarizáció speciális esete. Az 1,0 excentrikus elliptikusan polarizált hullám egy körkörösen polarizált hullám. Elliptikusan polarizált hullámok végtelen excentricitással. Lineárisan polarizált hullámok.
Antenna polarizáció
Most, hogy tisztában vagyunk a polarizált síkhullámú elektromágneses mezőkkel, az antenna polarizációját egyszerűen definiálhatjuk.
Antenna polarizáció Az antenna távoli mezőjének kiértékelése, a kapott kisugárzott mező polarizációja. Ezért az antennákat gyakran "lineárisan polarizált" vagy "jobbra forgó, cirkulárisan polarizált antennákként" sorolják fel.
Ez az egyszerű koncepció fontos az antennás kommunikáció szempontjából. Először is, egy vízszintesen polarizált antenna nem fog kommunikálni egy függőlegesen polarizált antennával. A reciprocitás tétele miatt az antenna pontosan ugyanúgy ad és vesz. Ezért a függőlegesen polarizált antennák függőlegesen polarizált mezőket adnak és vesznek. Ezért, ha megpróbálunk egy függőlegesen polarizált, vízszintesen polarizált antennát továbbítani, nem lesz vétel.
Általános esetben két lineárisan polarizált, egymáshoz képest egy szöggel ( ) elforgatott antenna esetén a polarizációs eltérésből adódó teljesítményveszteséget a polarizációs veszteségi tényező (PLF) írja le:
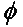
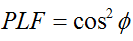
Tehát, ha két antenna azonos polarizációval rendelkezik, a sugárzó elektronmezeik közötti szög nulla, és nincs teljesítményveszteség a polarizációs eltérés miatt. Ha az egyik antenna függőlegesen, a másik pedig vízszintesen polarizált, a szög 90 fok, és nem történik teljesítményátadás.
MEGJEGYZÉS: A telefon fej feletti különböző szögekbe mozgatása megmagyarázza, miért javulhat néha a vétel. A mobiltelefon-antennák általában lineárisan polarizáltak, így a telefon elforgatása gyakran illeszkedik a telefon polarizációjához, ezáltal javítva a vételt.
A körkörös polarizáció számos antenna kívánatos tulajdonsága. Mindkét antenna körkörösen polarizált, és nem szenvednek jelveszteséget a polarizációs eltérés miatt. A GPS-rendszerekben használt antennák jobbra körkörösen polarizáltak.
Most tegyük fel, hogy egy lineárisan polarizált antenna cirkulárisan polarizált hullámokat vesz. Ezzel egyenértékűen tegyük fel, hogy egy cirkulárisan polarizált antenna lineárisan polarizált hullámok vételére törekszik. Mekkora az eredő polarizációs veszteségtényező?
Emlékezzünk vissza, hogy a cirkuláris polarizáció valójában két ortogonális, lineárisan polarizált hullám, amelyek 90 fokkal eltérnek a fázistól. Ezért egy lineárisan polarizált (LP) antenna csak a cirkulárisan polarizált (CP) hullám fáziskomponensét veszi. Ezért az LP antenna polarizációs eltérési vesztesége 0,5 (-3 dB) lesz. Ez igaz, függetlenül attól, hogy milyen szögben forgatják el az LP antennát. Tehát:
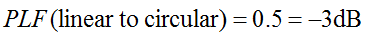
A polarizációs veszteségi tényezőt néha polarizációs hatásfoknak, antenna illesztési tényezőnek vagy antenna vételi tényezőnek is nevezik. Mindezek az elnevezések ugyanarra a fogalomra utalnak.
Közzététel ideje: 2023. dec. 22.







