Amikor arról van szóantennák, az embereket leginkább foglalkoztató kérdés az, hogy "Hogyan érhető el valójában a sugárzás?" Hogyan terjed a jelforrás által generált elektromágneses mező az átviteli vezetéken és az antenna belsejében, majd hogyan "leválik" az antennáról, szabad térhullámot képezve.
1. Egyvezetékes sugárzás
Tegyük fel, hogy a töltéssűrűség, qv-ben (Coulomb/m3) kifejezve, egyenletesen oszlik el egy a keresztmetszetű és V térfogatú kör alakú vezetékben, ahogy az az 1. ábrán látható.
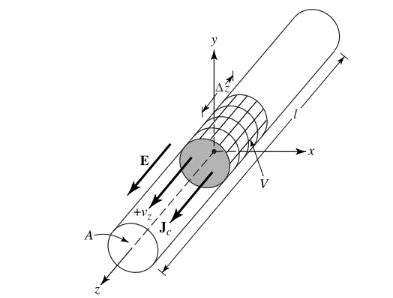
1. ábra
A V térfogatban lévő Q teljes töltés z irányban egyenletes Vz (m/s) sebességgel mozog. Bizonyítható, hogy a vezeték keresztmetszetén az áramsűrűség Jz:
Jz = qv vz (1)
Ha a vezeték ideális vezetőből készül, akkor a vezeték felületén mért áramsűrűség (Js):
Js = qs vz (2)
Ahol qs a felületi töltéssűrűség. Ha a vezeték nagyon vékony (ideális esetben a sugár 0), akkor a vezetékben folyó áram a következőképpen fejezhető ki:
Iz = ql vz (3)
Ahol ql (coulomb/méter) az egységnyi hosszra jutó töltés.
Főként vékony vezetékekkel foglalkozunk, és a következtetések a fenti három esetre vonatkoznak. Ha az áram időben változik, akkor a (3) képlet időbeli deriváltja a következő:
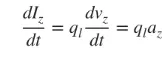
(4)
az a töltésgyorsulás. Ha a vezeték hossza l, akkor a (4) egyenlet a következőképpen írható fel:
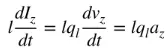
(5)
Az (5) egyenlet az áram és a töltés, valamint az elektromágneses sugárzás alapvető összefüggését írja le. Egyszerűen fogalmazva, a sugárzás létrehozásához időben változó áramnak vagy a töltés gyorsulásának (vagy lassulásának) kell lennie. Az áramot általában időharmonikus alkalmazásokban említjük, a töltést pedig leggyakrabban tranziens alkalmazásokban. A töltés gyorsulásának (vagy lassulásának) létrehozásához a vezetéket meg kell hajlítani, hajtogatni és szakaszossá kell tenni. Amikor a töltés időben harmonikus mozgásban oszcillál, periodikus töltésgyorsulást (vagy lassulást), vagy időben változó áramot is létrehoz. Ezért:
1) Ha a töltés nem mozdul el, akkor nincs áram és nincs sugárzás.
2) Ha a töltés állandó sebességgel mozog:
a. Ha a vezeték egyenes és végtelen hosszú, akkor nincs sugárzás.
b. Ha a vezeték meg van hajlítva, hajtva vagy szakaszos, ahogy a 2. ábrán látható, sugárzás keletkezik.
3) Ha a töltés időben oszcillál, akkor a töltés akkor is sugárzik, ha a vezeték egyenes.
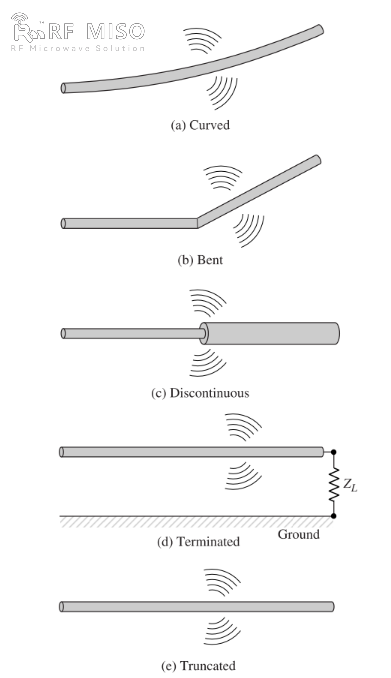
2. ábra
A sugárzási mechanizmus kvalitatív megértéséhez egy impulzusos forrást vizsgálunk, amely egy nyitott vezetékhez van csatlakoztatva, és amelynek nyitott végén egy terhelésen keresztül földelhető, ahogy az a 2(d) ábrán látható. Amikor a vezetéket kezdetben gerjesztjük, a vezetékben lévő töltéseket (szabad elektronokat) a forrás által generált elektromos térvonalak mozgásba hozzák. Ahogy a töltések a vezeték forrás felőli végén gyorsulnak, és a végén visszaverődve lassulnak (negatív gyorsulás az eredeti mozgáshoz képest), sugárzó tér keletkezik a végein és a vezeték többi részén. A töltések gyorsulását egy külső erőforrás valósítja meg, amely mozgásba hozza a töltéseket, és létrehozza a hozzájuk tartozó sugárzási teret. A vezeték végein a töltések lassulását az indukált térrel kapcsolatos belső erők biztosítják, amelyet a vezeték végein koncentrált töltések felhalmozódása okoz. A belső erők energiát nyernek a töltés felhalmozódásából, mivel annak sebessége nullára csökken a vezeték végein. Ezért a töltések gyorsulása az elektromos tér gerjesztése miatt, valamint a töltések lassulása a vezeték impedanciájának folytonossági hiánya vagy sima görbéje miatt az elektromágneses sugárzás keletkezésének mechanizmusai. Bár mind az áramsűrűség (Jc), mind a töltéssűrűség (qv) forrástagok a Maxwell-egyenletekben, a töltést alapvetőbb mennyiségnek tekintik, különösen tranziens mezők esetén. Bár a sugárzásnak ezt a magyarázatát főként tranziens állapotokra használják, az állandósult állapotú sugárzás magyarázatára is használható.
Ajánlj több kiválót isantenna termékekáltal gyártottRFMISO:
2. Kétvezetékes sugárzás
Csatlakoztasson egy feszültségforrást egy antennához csatlakoztatott kétvezetékes távvezetékhez, ahogy a 3(a) ábra mutatja. A kétvezetékes vezetékre kapcsolt feszültség elektromos mezőt hoz létre a vezetők között. Az elektromos mező vonalak hatnak a vezetőkhöz csatlakoztatott szabad elektronokra (amelyek könnyen elválaszthatók az atomoktól), és mozgásra kényszerítik azokat. A töltések mozgása áramot generál, ami viszont mágneses mezőt generál.
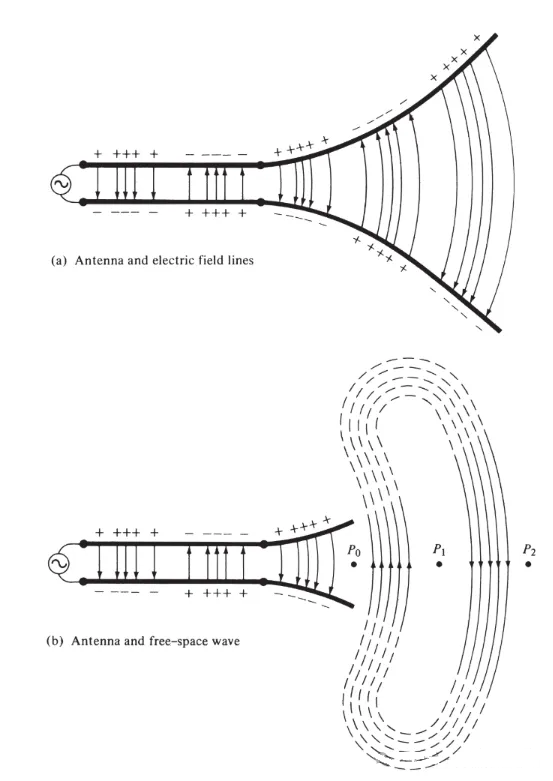
3. ábra
Elfogadtuk, hogy az elektromos térvonalak pozitív töltésekkel kezdődnek és negatív töltésekkel végződnek. Természetesen kezdődhetnek pozitív töltésekkel és végtelenben is végződhetnek; vagy kezdődhetnek végtelenben és negatív töltésekkel végződhetnek; vagy alkothatnak olyan zárt hurkokat, amelyek sem nem kezdődnek, sem nem végződnek töltéssel. A mágneses térvonalak mindig zárt hurkokat alkotnak az áramvezető vezetők körül, mivel a fizikában nincsenek mágneses töltések. Néhány matematikai képletben ekvivalens mágneses töltéseket és mágneses áramokat vezetnek be, hogy bemutassák a teljesítményt és a mágneses forrásokat magában foglaló megoldások kettősségét.
A két vezető között húzott elektromos térerősség-vonalak segítenek bemutatni a töltéseloszlást. Ha feltételezzük, hogy a feszültségforrás szinuszos, akkor a vezetők közötti elektromos tér várhatóan szintén szinuszos lesz, a forráséval megegyező periódussal. Az elektromos térerősség relatív nagyságát az elektromos térerősség-vonalak sűrűsége jelöli, a nyilak pedig a relatív irányt (pozitív vagy negatív) jelzik. A vezetők között időben változó elektromos és mágneses mezők keletkezése elektromágneses hullámot hoz létre, amely a távvezeték mentén terjed, ahogy az a 3(a) ábrán látható. Az elektromágneses hullám a töltéssel és a hozzá tartozó árammal együtt belép az antennába. Ha eltávolítjuk az antennaszerkezet egy részét, ahogy az a 3(b) ábrán látható, akkor az elektromos térerősség-vonalak nyitott végeinek "összekapcsolásával" (a szaggatott vonalakkal jelölve) szabad térbeli hullám hozható létre. A szabad térbeli hullám szintén periodikus, de az állandó fázisú P0 pont fénysebességgel kifelé mozog, és λ/2 távolságot (P1-ig) tesz meg fél idő alatt. Az antenna közelében az állandó fázisú P0 pont gyorsabban mozog, mint a fénysebesség, és az antennától távol eső pontokban megközelíti a fénysebességet. A 4. ábra a λ∕2 antenna szabad térbeli elektromos tér eloszlását mutatja t = 0, t/8, t/4 és 3T/8 időpontokban.
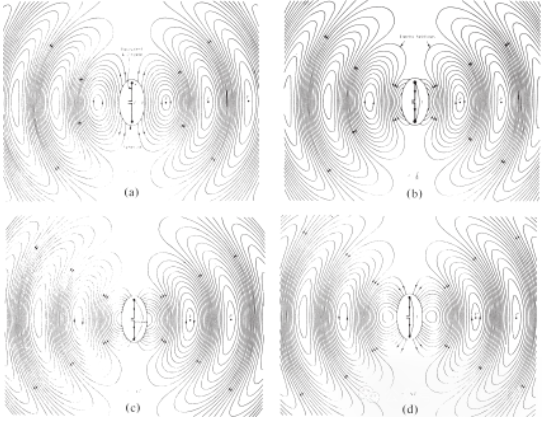
4. ábra A λ∕2 antenna szabadtérbeli elektromos téreloszlása t = 0, t/8, t/4 és 3T/8 időpontokban
Nem ismert, hogyan válnak le a vezetett hullámok az antennáról, és hogyan alakulnak ki végül a szabad térben terjedésük. A vezetett és a szabad térben terjedő hullámokat összehasonlíthatjuk a vízhullámokkal, amelyeket egy nyugodt vízbe ejtett kő vagy más módon okozhat. Amint a vízben megindul a zavar, vízhullámok keletkeznek, és kifelé terjedni kezdenek. Még ha a zavar meg is szűnik, a hullámok nem állnak meg, hanem tovább terjednek előre. Ha a zavar továbbra is fennáll, folyamatosan új hullámok keletkeznek, és ezeknek a hullámoknak a terjedése elmarad a többi hullámétól.
Ugyanez igaz az elektromos zavarok által keltett elektromágneses hullámokra is. Ha a forrásból származó kezdeti elektromos zavar rövid ideig tart, a keletkező elektromágneses hullámok a távvezetéken belül terjednek, majd belépnek az antennába, és végül szabad térben kisugároznak, annak ellenére, hogy a gerjesztés már nincs jelen (ahogy a vízhullámok és az általuk keltett zavar is). Ha az elektromos zavar folyamatos, az elektromágneses hullámok folyamatosan léteznek, és a terjedés során szorosan követik őket, ahogyan az az 5. ábrán látható bikonikus antennán is látható. Amikor az elektromágneses hullámok távvezetékeken és antennákon belül vannak, létezésük összefügg a vezetőben lévő elektromos töltéssel. Amikor azonban a hullámok kisugárzódnak, zárt hurkot alkotnak, és nincs töltés, amely fenntartaná a létezésüket. Ez arra a következtetésre vezet, hogy:
A tér gerjesztéséhez a töltés gyorsítása és lassítása szükséges, de a tér fenntartásához nincs szükség a töltés gyorsítására és lassítására.
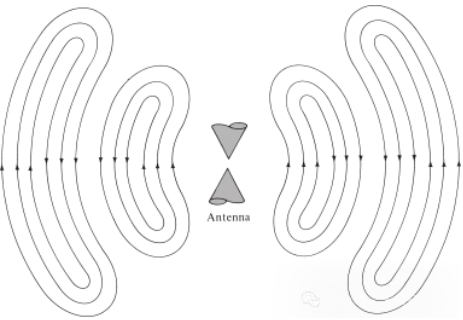
5. ábra
3. Dipólussugárzás
Megpróbáljuk elmagyarázni azt a mechanizmust, ahogyan az elektromos erővonalak elszakadnak az antennától és szabadtér-hullámokat hoznak létre, és példaként a dipólantennát vesszük. Bár ez egy leegyszerűsített magyarázat, lehetővé teszi az emberek számára, hogy intuitív módon lássák a szabadtér-hullámok keletkezését. A 6(a) ábra a dipólus két karja között keletkező elektromos erővonalakat mutatja, amikor az elektromos erővonalak λ∕4 távolsággal kifelé mozdulnak el a ciklus első negyedében. Ebben a példában tegyük fel, hogy a kialakult elektromos erővonalak száma 3. A ciklus következő negyedében az eredeti három elektromos erővonal további λ∕4 távolsággal mozdul el (összesen λ∕2 távolsággal a kiindulási ponttól), és a vezető töltéssűrűsége csökkenni kezd. Úgy tekinthető, hogy ellentétes töltések bevezetésével jön létre, amelyek a ciklus első felének végén kioltják a vezető töltéseit. Az ellentétes töltések által létrehozott elektromos erővonalak mérete 3, és λ∕4 távolságot mozdulnak el, amit a 6(b) ábrán szaggatott vonalak ábrázolnak.
A végeredmény az, hogy három lefelé irányuló elektromos térvonal található az első λ∕4 távolságban, és ugyanannyi felfelé irányuló elektromos térvonal a második λ∕4 távolságban. Mivel az antennán nincs nettó töltés, az elektromos térvonalakat kényszeríteni kell, hogy elváljanak a vezetőtől, és zárt hurkot alkossanak. Ez a 6(c) ábrán látható. A második felében ugyanaz a fizikai folyamat következik be, de megjegyzendő, hogy az irány ellentétes. Ezután a folyamat megismétlődik, és a végtelenségig folytatódik, a 4. ábrához hasonló elektromos téreloszlást kialakítva.
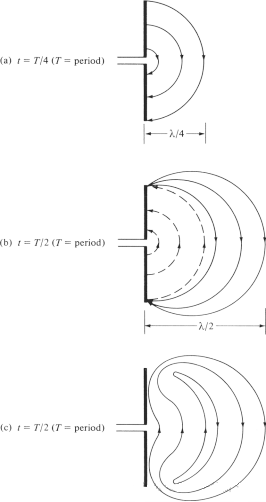
6. ábra
Az antennákról bővebben itt olvashat:
Közzététel ideje: 2024. június 20.










